Pi Sayısını Olasılık Kullanarak Tahmin Edebilen Harika Bir Yöntem: Buffon'un İğnesi

şöyle ki:
yan yana dizilmiş eşit genişlikte (genişlik: t) tahta parçalarının üzerine l uzunluğunda
calculus kullanarak, bu iğnenin herhangi iki komşu tahta parçası arasındaki çizginin üzerinden geçecek şekilde düşme ihtimali (p);
p = 2l/t*pi olarak bulunur. (1)
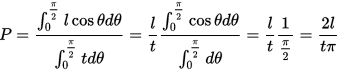
şimdi birden daha çok deneme yaptığımızı varsayalım. toplam deneme sayısı n, çizgi üzerine düşen iğne sayısı h olsun.
örnek:
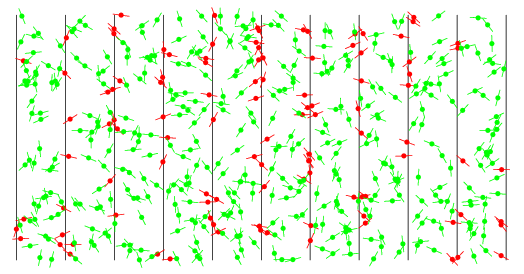
bu durumda p = h/n olacaktır. (2)
1 ve 2 numaralı eşitlikleri kullanarak,
p = 2l/t*pi = h/n -----> pi = 2l*n/t*h olarak bulunur. (3)
yeteri kadar deneme sonrasında, 3 numaralı eşitliği kullanarak, pi sayısına yeterince yaklaşım sağlanabilir. deneme sayısı sonsuza ıraksarken, söz konusu olasılık pi sayısına yakınsar.
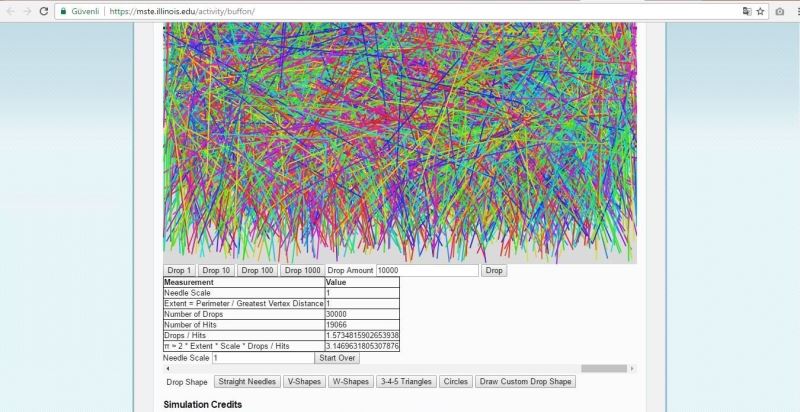
simülasyon :
şuradaki simülasyonu kullanarak, söz gelimi 30,000 atış sonrasında (19,066 tanesi çizgi üzerinde) elde edilen yaklaşık pi değeri,
pi = 3,14696318... olarak bulunabilir.