Öklid, 1'i Neden Sayı Olarak Kabul Etmedi?

0 sayısının 600'lü yıllarda yaşamış matematikçi brahmagupta'ya kadar kullanılmadığını ve bir sayı olarak kabul edilmediğini çoğu insan bilir. tamamen aynı olmasa da benzer şekilde 1 sayısının da bir zamanlar antik yunan ve iskenderiye gibi matematiğin çılgınlarcasına geliştirildiği yerlerde sayı olarak kabul edilmezdi. 1 sayısını sayı olarak görmeyen kişilerden en önemlisi ise günümüzde geometri dediğimiz matematik alanının, daha doğrusu matematiğin en temel dayanak noktasının neredeyse tek başına sorumlusu olan öklid isimli matematikçidir.
aslında bu durum matematikteki sayı kavramının zamanla evrimleşmiş, gelişmiş, karmaşıklaşmış ve değişmiş olmasından kaynaklı. matematikte bazı aksiyomlar hariç her şeyin çok net ve keskin tanımı vardır ve bu tanımlar mümkün olan en özel biçimde yapılır ve genellikle bu tanımlar mantık dilinde yazılabilecek kadar net olur.
buna örnek olarak eşitliği, örnek göstermek adına da küme eşitliğini ele alalım. aynı elemanlara sahip olan kümelerin birbirlerine eşit kümeler olduğunu biliriz ve bize bu tanım gayet açık bir tanımmış gibi görünür ancak matematik bu şekilde işlemez. yani "aynı elemanları olan kümeler eşit işte kardeşim" diyerek matematiksel bir tanım yapmış olmayız. küme eşitliğinin matematiksel bir tanımı vardır ve o tanım bu şekilde görünür:
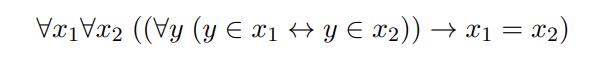
görseldeki yazı matematiksel mantık dilinde yazılmış bir aksiyomdur ve türkçe çevirisi tam olarak "her x1 ve her x2 kümeleri için, her y kümesi ancak ve ancak y kümesi x1 kümesinin elemanıyken x2 kümesinin elemanı olabiliyor ise x1 kümesi ile x2 kümesi eşit kümelerdir" şeklindedir. bu örnekten tanım yapma işinin aslında öyle basit ve genel bir şey olmadığının anlaşıldığını düşünüyorum.
sayılardan devam edelim...
matematiksel bakımdan sayı dediğimiz şeylerin günlük hayatta herkesin net olarak anlayabileceği genel bir tanımı yoktur çünkü matematikte belirli benzerliklere sahip her türden konseptin özelliklerini sağlayan genel bir tanım yapmak istenen bir şey olsa da günlük hayat için çoğunlukla mümkün değildir. mesela biri bana gelip "matematikte sayı ne ki" diye sorsa aşağıdaki görseli açıp "complex yazanın içindeki her şeye sayı deniyor işte" cevabını veririm ve bu bir çeşit gündelik hayat tanımı olur ancak ne karşımdaki kişi dediğimden bir şey anlamış olur ne de ben o kişiye doğru düzgün bir tanım vermiş olurum:
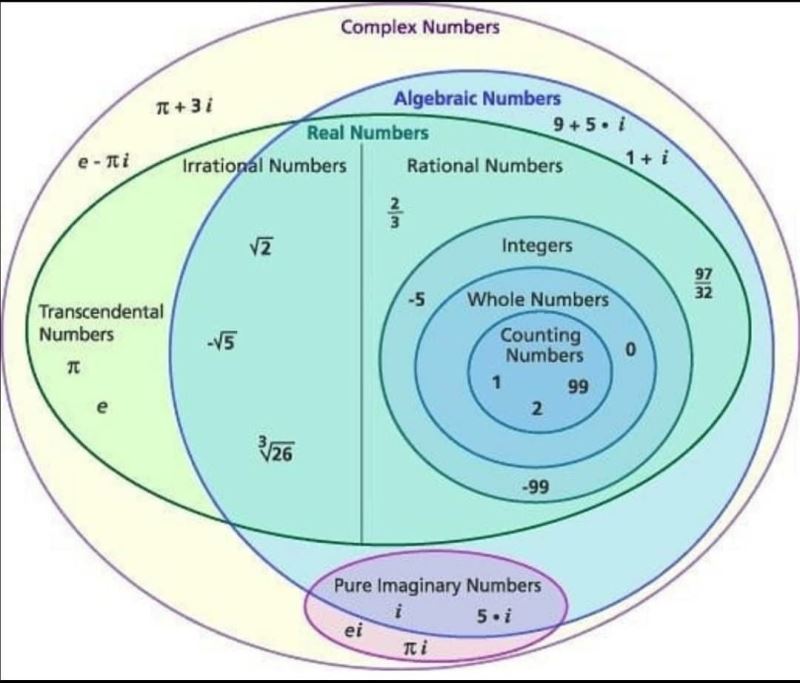
bu sebepten günlük hayatta pek düşünmeden kullandığımız matematiksel konseptlerin, yani mesela sayıların tanımları, sayı derken özel olarak kast ettiğimiz sayıların özelliklerine ve niteliklerine göre yapılır. bu özellikler çok yoğun ve uzun uğraşlar sonucunda matematikçiler tarafından tespit edilip sınıflandırılmış ve insanlığın bilgi dağarcığına yerleştirilmiş özelliklerdir. ancak bu insanlar bu işleri yapabilmek için hayatlarını adayan ve bir ömürlük eğitimlerini kullanarak çalışan insanlar olduklarından bu insanların yaptıkları işleri temel eğitim alan çocuklara ve hatta yetişkinlere ayrıntılı biçimde anlatmak pratik değildir. bu sebepten biz bu insanlardan aldığımız derin bilgileri temel eğitimlerde çocuklara ve uzmanlık alanı matematik olmayan insanlara hap bilgi diyebileceğimiz "sorgulama işte" mantığıyla ezberletiriz.
ancak bu durum her zaman bu şekilde değildi çünkü insanlık her zaman şu an sahip olduğumuz bilgi birikimine sahip değildi. mesela yukarıda paylaştığım görselde gördüğümüz kümeler 1800'lü yıllara kadar kimse tarafından görülmedi çünkü küme fikri 1870 yılında richard dedekind ve georg cantor isminde iki sıkıntılı matematikçi tarafından o zamana kadar insanlık tarafından geliştirilmiş bütün matematik birikimi kullanılarak ortaya atıldı. yani aslında günümüzde biliyor ve anlıyormuş gibi kabul edip geçtiğimiz kavramlar öklid'den cantor'a kadar binlerce yıl tartışmalar ve ilerlemelerle ortaya çıktılar.
öklid'in yaşadığı dönemde ise bırak kümeleri sıfır bile yoktu. sıfır bir yana, daha önce riemann hipotezini açıkladığım yazıda belirttiğim gibi negatif sayılar bile yoktu. o dönemlerde insanlar sayıları günümüzdeki gibi değil, belirli bir grubu, yani çokluğu temsil eden soyut cisimler olarak görüyorlardı.
öklid'in 1'i sayı olarak görmemesindeki mantığı da aslında bu kadar basit bir mantık değil. sayılar kuramına hakim olanlar bilirler ki bir hariç tüm doğal sayılar ya asaldır ya da iki asal sayının çarpımının sonucudur. yani basitçe herhangi bir doğal sayı alırsak ve ona x sayısı dersek x sayısı ya asaldır ya da belirli asal sayıların çarpımının bir sonucudur.
eğer x sayısı asal bir sayıysa zaten o sayıyı başka doğal sayıların çarpımı olarak yazmanın bir yolu yoktur. eğer x sayısı asal bir sayı değilse de o zaman x sayısını asal sayıların çarpımı olarak yazmanın yalnızca bir yolu mümkündür. bu yol da asal çarpanlara ayırma yöntemidir.
örneğin 44 sayısını ele alalım. 44 sayısı asal bir sayı olmadığı için kesin olarak asal sayıların çarpımından meydana gelmiştir. eğer biz bu sayının hangi asal sayıların çarpımından meydana geldiğini anlamak istersek yapmamız gereken şey 2'den başlayarak bu sayıyı bölebildiğimiz kadar asal sayıya bölerek ilerlemektir.
44/2 = 22
22/2 = 11
11/11 = 1
yukarıda görüldüğü üzere 44 sayısı 2x2x11 şeklinde 2 ve 11 asallarının çarpımlarından oluşmuştur. bu durumda bu sayının asal çarpım şeklinde gösterilmesinin tek yolu 2x2x11 olur ve başka hiçbir asal çarpım şeklinde gösterilemez.
gelelim 1'in asal olmamasının ve öklid'e göre sayı bile olmamasının sebebine.
tüm doğal sayıların asal çarpanlardan oluştuğunu ve her doğal sayı için bu çarpanların eşsiz bir dizilimi olduğunu söylemiştik. eğer biz gidip de 1'in bir asal sayı olduğunu kabul edersek sayıların bu belirgin özelliği ortadan kalkar ve sayılar bu özelliklerini kaybettiklerinden sayıları tanımlamak çok daha zor bir hale gelir.
1'i asal sayı kabul etmek bu özelliği bozar çünkü mesela eğer 1 sayısını asal kabul edersek 2x2x11 örneğindeki eşsiz formülü hem 1x1x2x2x11 şeklinde hem de 1x2x2x11 şeklinde yazabiliriz. bu durumda hiçbir doğal sayının asal çarpan formülü eşsiz olmaz çünkü aynı mantığı tüm doğal sayılara uygulayabiliriz. bu durumda 1'in asal sayı kabul edilmesi bizim sayı tanımı yapma konusundaki işimizi çok zorlaştırır ve çıkmaza gireriz. ancak eğer 1'i asal sayı olarak kabul etmezsek sorun çözülür ve gönül rahatlığıyla matematik yapmaya devam edebiliriz.
tüm doğal sayılar ya asaldır ya da asal sayıların çarpımından oluşur demiştik. öklid döneminde zaten 1/4, 1/8 gibi tam sayı olmayan kesirli ifadeler ve doğal sayılar dışında bir sayı konsepti olmadığı için 1 sayısı bir sayı olarak kabul edilmemiştir çünkü 1 hem asal değildir hem de asal sayıların çarpımından oluşmaz.
bu durum 1600'lü yıllara kadar, yani insanlık tarihinin büyük bir bölümü boyunca sürmüş, modern çağın matematik birikimiyle oluşturulan tanımlar ile de geçerliliğini kaybetmiştir.
kaynakça ve ileri okuma: sayılar wiki, kümeler kuramı wiki, scientificamerican asal sayılar ve 1, matematikçilerin sayı tanımını tartıştıkları bir forum, 1'in sayı kabul edilmediğinin tarihi kaynağını söyleyen bir dergi