Neden Sadece 5 Farklı Zar Çeşidi Yapmak Mümkündür?

eğer zar dediğimiz şeyin üç boyutlu düzlemde eşit alana sahip geometrik yüzeyleri olan bir cisim olduğunu kabul edersek sadece 5 farklı zar çeşidi yapılabilir.
peki bu ne demek?
günlük hayatta en çok kullanılan zar olan küp zarın şeklini düşünelim. bu zarda altı farklı sayı gelme ihtimali vardır ve bu ihtimaller zarın mükemmel bir şekilde hilesiz olduğunu düşündüğümüz durumda birbirine eşittir çünkü zarın her bir yüzü diğeriyle aynıdır. bunun sebebi zarın bir küp olmasıdır.

ancak eğer kenarları birbirine aynı olan başka bir zar yapmak isteseydik yapabilirdik. tek bir koşulla. eğer küp dışında bir zar yapmak isteseydik sadece ve sadece 4 farklı zar yapma imkanımız olurdu:
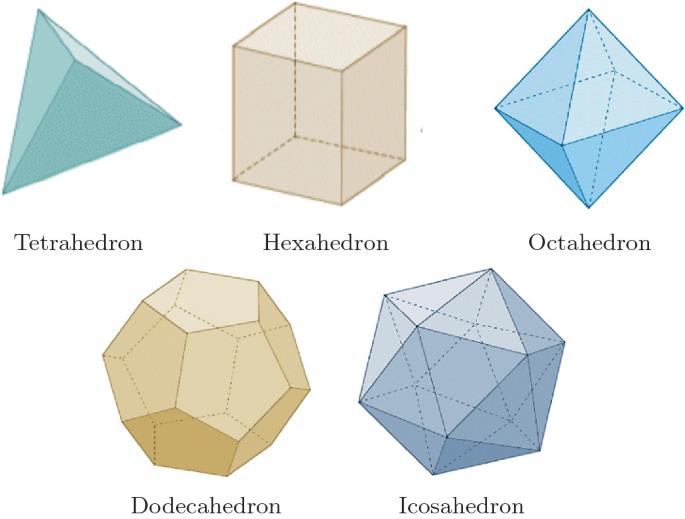
görseldeki cisimlerin her biri üç boyutludur ve hepsi birbirine eşit alanlara sahip yüzeylerin bir araya gelmesiyle oluşmuş cisimlerdir. bu cisimlere platon katıları denir. eğer bu cisimlerden farklı bir zar yapmak ister ve bu zarın her yüzeyinin alanının diğerleriyle eşit olması için çabalarsanız başaramazsınız.
peki neden?
eğer üç boyutlu bir geometrik cismi alır, bu cismin yüzey sayısı ile köşe sayısını toplar ve bu sayıdan köşeleri birleştiren kenar sayısını çıkarırsanız daima 2 sonucunu bulursunuz.
bu olaya yabancı literatürde euler characteristic denir. türkçe çevirisi sanırım yok, bu sebepten ben euler karakteristiği diyeceğim.
euler karakteristiği:
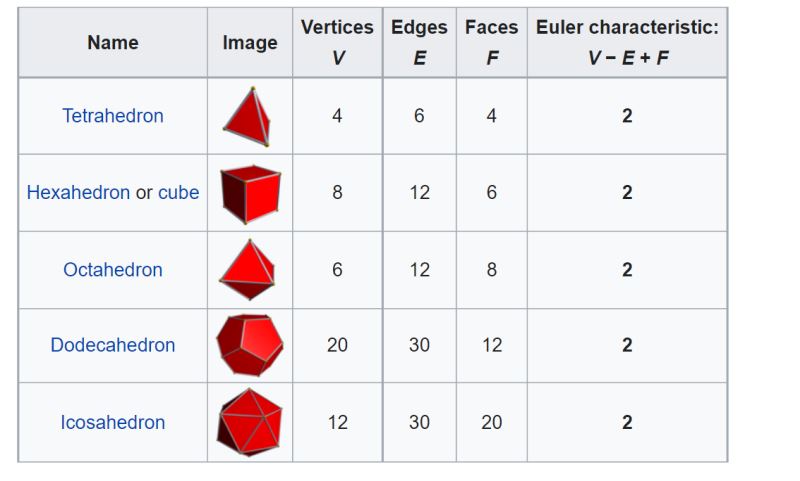
şimdi diyelim ki üç boyutlu bir cismin kenarlarını sayıyoruz. bu cismin her bir yüzü ile diğer yüzü birbiriyle bitişik olacağından bu cismin kenarlarını saydığımızda bulacağımız sonuç bu cismi ayrı ayrı inceleseydik bulacağımız sonuçtan farklı olurdu.
örneğin bir küp düşünelim.
eğer bir küpün sahip olduğu kenarları sayarsak 12 sonucunu buluruz. ancak bu küpün yüzeylerini ayırır ve her bir yüzeyi oluşturan karelerin kenarlarını ayrı ayrı sayarsak 4x6=24 işleminden 24 kenar buluruz.
bu noktada bir şeyle karşılaşıyoruz.
küpü oluşturan kareleri ayrı ayrı incelediğimizde bulduğumuz kenar sayısı, küpün kendisini incelediğimizde bulduğumuz kenar sayısının iki katına eşit çıkıyor.
diyelim ki küp yerine bir tetrahedronu, yani 4 farklı üçgen yüzeyin bir araya getirilmesiyle oluşturulmuş üç boyutlu cismi inceliyoruz:
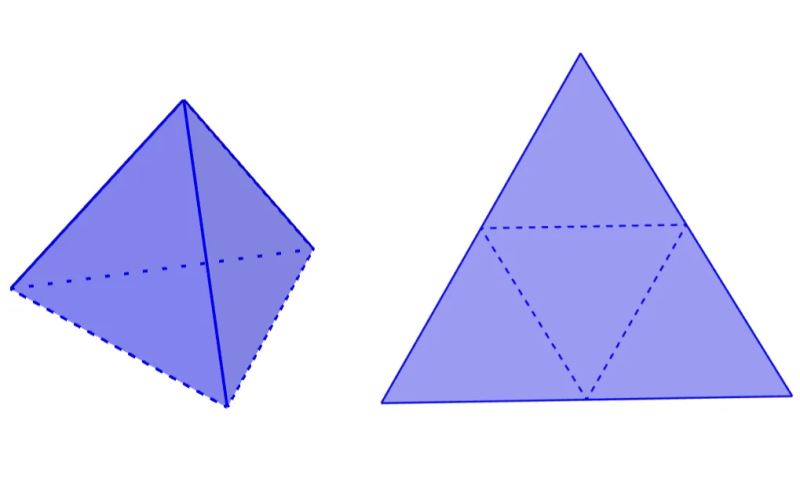
eğer tetrahedron'u oluşturan üçgenlerin kenarlarını ayrı ayrı sayarsak 12 kenar sonucuna varırken, bu üçgenlerle üç boyutlu bir cisim oluşturduğumuzda ortaya çıkan cismin kenarlarını sayarsak 6 kenar sonucuna varıyoruz.
bu noktada küp ve tetrahedron arasında bir benzerlik bulduk.
önce euler karakteristiğini formülize edelim:
yüzey sayısı = f
köşe sayısı = v
kenar sayısı = e
her geometrik cisim için: v + f - e = 2
biz küp ve tetrahedron'da ayrı ayrı incelendiklerinde kenar sayılarının iki katına çıktığını görmüştük.
v + f -e = 2 formülündeki sembolleri bu duruma uyarlayabilmek için bir küpün her bir köşesinin kaç kenar ile bağlantılı olduğuna bakalım:
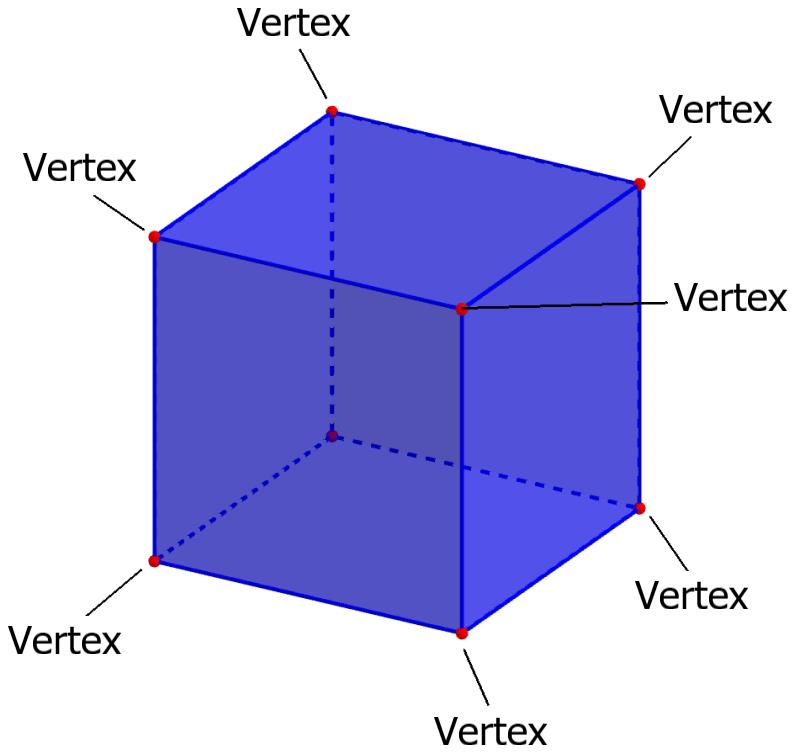
şekilde görülebileceği üzere küpün her bir köşesine 3 kenar bağlantılıdır.
bir köşeye bağlantılı kenar sayısına ek diyelim.
bu durumda küp için şöyle bir formüle erişiriz: (v) (ek) = 2e
yani eğer köşe sayısı ile köşelere değen kenar sayısını çarparsak kenar sayısının iki katını buluruz.
küp için: 8 x 3 = 24
tetrahedron için: 4x3 = 12
şimdi aynı formülü başka bir biçimde tekrar işimize yarayacak şekilde uyarlayalım.
bir cismi oluşturan yüzeydeki toplam kenar sayısına fk diyelim.
eğer küpü yüzeylerine ayırırsak ve toplam kenar sayısını hesaplarsak yaptığımız işlemi şu şekilde formüle dönüştürebiliriz:
(f) (fk) = 2e
yani yüzey sayısı ile yüzeyleri oluşturan kenarların toplamı bu cisimdeki kenarların iki katına eşit olacaktır.
şimdi v + f - e = 2 formülünü yukarıdaki formüller şeklinde yazalım:
v = 2e/ek
f = 2e/fk
v + f = 2 + e
böylelikle:
(2e/ek) + (2e/fk) = 2 + e
yani eğer üç boyutlu bir cisimdeki kenar sayısının iki katının bu cisimdeki bir köşeye bağlantılı kenar sayısına bölümü ile bu cisimdeki kenar sayısının iki katının bu cisimdeki bir yüzeyin toplam kenar sayısına bölümü ile toplarsak elde edeceğimiz sonuç bu cisimdeki kenar sayısının iki fazlası olur.
şimdi denklemde iki tarafı da 2e sayısına bölelim:
(2e/ek) + (2e/fk) = 1/ek + 1/fk ve (2+e)/2e = 1/e + 1/2
böylelikle:
1/ek + 1/fk = 1/e + 1/2
bir geometrik cisimdeki kenar sayısı daima pozitif olacağından yukarıdaki denklemin sağ tarafındaki sayının 1/2 sayısından büyük bir sayı olacağı sonucuna varırız.
böylelikle: 1/ek + 1/fk > 1/2
burada oldukça estetik bir şey keşfetmiş olduk.
ek sayısı bir geometrik cisimdeki kenar sayısını, fk sayısı ise üç boyutlu bir cisimdeki köşelere bağlı olan kenar sayısını temsil ediyor demiştik.
bir geometrik cisimde sahip olabileceğimiz en düşük kenar sayısı 3'tür çünkü en az kenarı olan geometrik cisim üçgendir. tam olarak bu sebepten en az köşeye sahip üç boyutlu cisim üçgenlerle yapıldığından, köşelerin bağladığı kenar sayısı da üçten küçük olamaz.
bu durumda hem ek sayısı hem de fk sayısı ya üç olacak ya da üçten küçük olacaktır.
şimdi yukarıdaki eşitsizliğimize dönelim.
1/ek + 1/fk < 1/2 demiştik.
bu durumda ek ve fk sayılarının 3 ya da 3'ten büyük olmaları gerektiğini biliyoruz.
yukarıdaki eşitsizliğe uyabilecek sınırlı sayıda ek + fk değeri vardır.
bu değerler şu şekildedir:
1-> ek = 3 ve fk = 3, böylelikle 1/3 + 1/3 > 1/2
2 -> ek = 4 ve fk = 3, böylelikle 1/4 + 1/3 > 1/2
3-> ek = 3 ve fk = 4, böylelikle 1/3 + 1/4 > 1/2
4-> ek = 5 ve fk = 3, böylelikle 1/5 + 1/3 > 1/2
5-> ek = 3 ve fk = 5, böylelikle 1/3 + 1/5 > 1/2
yukarıdaki değerlerin her biri bir platon katısına denk gelmektedir.
eğer platon katılarının her birini incelerseniz birinci değerin tetrahedrona, ikinci değerin küpe, üçüncü değerin oktahedrona, dördüncü değerin dodekahedrona, beşinci değerin de ikosahedrona eşit olacağını görürsünüz.
eğer herhangi bir farklı değer verir ve 6. bir zar yapmaya çalışırsanız vereceğiniz bu değerlerin toplamı 1/2 sayısından düşük olur ve platon objelerinin her birinin gösterdiği (v)(ek) = 2e ve (f)(fk) = 2e özelliğini göstermez. bu durumda elde edeceğiniz cismin her yüzü birbirine eşit olmaz.
platon katıları hakkında detaylı bilgi için: wiki linki
yukarıda gösterdiğim işlemlerin kanıtı için: makale



