Nasıl Olur da Bir Sonsuzluk Diğerinden Daha Büyük Olabilir?

bir sonsuzluğun başka bir sonsuzluktan büyük olabiliyor olması, kümeler üzerine çılgınlar gibi çalışan alman matematikçi georg cantor tarafından 1891 yılında köşegen yöntemi ile kanıtlanmıştır.

cantor'un kanıtının ardından sonsuzluk kavramı eşit boyuttaki sonsuzluklar ve eşit boyutta olan sonsuzluklardan büyük olan sonsuzluklar olarak ikiye ayrılmıştır.

birbirine eşit olan sonsuzluklara sayılabilir sonsuz ismi verilirken bu sonsuzluklardan büyük olan sonsuzluklara ise sayılamaz sonsuz ismi verilmiştir.

peki böyle bir şey nasıl mümkün olabilir?

bu konsepti anlayabilmek için öncelikle sonsuzluk denilen şeyin ne olduğu ve sayılabilir sonsuzlukların nasıl her zaman eşit büyüklükte olduğu hakkında bilgi sahibi olmak gerekir.

sonsuzluk kümeler gibi matematiksel nesnelerin sahip olabileceği bir sıfattır. sonsuz isminde bir sayı, şekil ya da nesne yoktur. nasıl kırmızı araba dediğimiz zaman kırmızı kelimesini bir nesne olarak değil de, bir nesnenin herhangi bir özelliğini belirten bir kavram olarak kullanıyorsak, sonsuzluk da tamamen aynı şekilde özellik belirleyen bir kavramdan ibarettir.

örneğin doğal sayılar ve tam sayılar kümeleri sonsuz elemana sahip kümelerdir.

çünkü siz bana bu iki kümenin herhangi bir elemanının ismini söylerseniz, mesela x sayısı derseniz, ben size x sayısının da ilerisinde bulunan x+1 ya da x-1 isminde bir sayı olduğunu söyleyebilirim. siz ne kadar denerseniz deneyin, en büyük doğal sayıyı, diğer bir deyişle son doğal sayıyı bulamazsınız çünkü doğal sayılar kümesinde daima bu sayıdan büyük başka bir sayı daha vardır.

doğal sayılar ve tam sayılar kümeleri karşılaştırıldığında ilk bakışta tam sayılar kümesinin doğal sayılar kümesinden daha büyük bir küme olduğu çıkarımı yapılabilir. çünkü doğal sayılar kümesinde sadece pozitif tam sayılar bulunurken tam sayılar kümesinde hem negatif hem de pozitif tam sayılar bulunur.

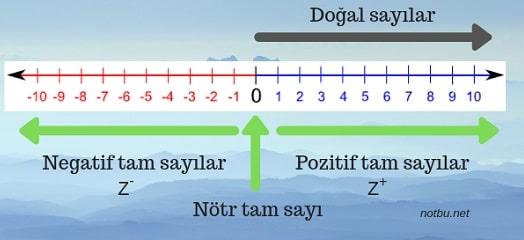
bu durumda göze doğal sayılar kümesindeki her eleman için tam sayılar kümesinde bir fazla eleman varmış gibi gelir.

örneğin doğal sayılar kümesindeki 1 elemanı için tam sayılar kümesinde 1 ve -1 elemanı, doğal sayılar kümesindeki 2 elemanı için tam sayılar kümesinde 2 ve -2 elemanı vardır.

bu şekilde elemanları saymayı sürdürürsek kolaylıkla tam sayılar kümesindeki eleman sayısının doğal sayılar kümesindeki eleman sayısından iki kat fazla olduğu yanılgısına düşeriz.

iki kümenin elemanları da sonsuz olduğundan, uygulamamız gereken yöntem hilbert oteli probleminde yaptığımıza benzer bir listeleme yöntemidir.

şimdi iki kümenin elemanlarını eşleyerek eleman sayıları arasındaki büyüklük farkını bulmayı deneyelim. bunu yapabilmek için de hiç matematik bilmeyen birinin bile kolaylıkla anlayabileceği bir fonksiyon tanımlayalım.

yapacağımız şey şu.

doğal sayılar kümesindeki her tek sayıyı tam sayılar kümesindeki pozitif bir sayıya, doğal sayılardaki her çift sayıyı ise tam sayılar kümesindeki negatif bir sayıya eşleyeceğiz.

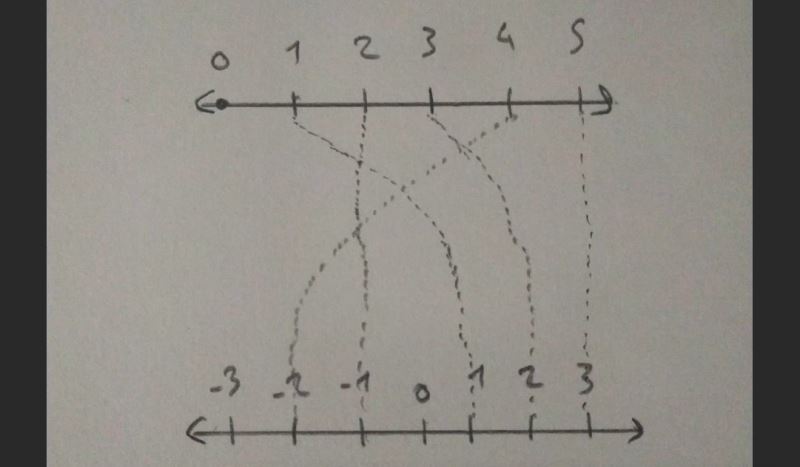
doğal sayılar kümesinde sonsuz tek sayı ve sonsuz çift sayı bulunduğu için tam sayılar kümesindeki hiçbir eleman boş kalmayacaktır. dolayısıyla doğal sayılar kümesinin eleman sayısı ile tam sayılar kümesinin sayısı her ne kadar tam sayılar kümesi daha büyükmüş gibi görünse de eşittir.

özetle sayılabilir sonsuzluk dediğimiz kavram aslında "birbiriyle eşlenebilir elemanlara sahip sonsuzluk" anlamına gelir.

peki eğer bütün elemanları bu şekilde eşleştirebiliyorsak, nasıl oluyor da bazı sonsuzluklar diğerlerinden daha büyük olabiliyor?

eğer iki kümenin her bir elemanı birbiriyle eşleşebiliyorsa bu kümeler eşit büyüklüktedir demiştik. bu sebepten sorumuzun cevabı, eşleştirilemeyecek sayılar içeren kümelerde yatar. bu kümelerden biri de reel sayılar kümesidir.

reel sayıların özelliklerinden biri irrasyonel sayılar'ı içinde bulundurmasıdır. yani her irrasyonel sayı aynı zamanda bir reel sayıdır.

irrasyonel sayı da virgülden sonraki haneleri sonsuza kadar giden sayılardır. örneğin pi sayısı bir irrasyonel sayıdır.

şimdi sayılamaz sonsuzluğun ne olduğunu anlayabilmek için reel sayılar kümesi ile doğal sayılar kümesini eşlemeye çalışalım.

öncelikle sonsuz uzunlukta bir kağıt alıyor ve bu kağıda yukarıdan aşağı dikey inecek biçimde bütün doğal sayıları alt alta sonsuza dek yazıyoruz.

daha sonra alt alta yazdığımız her bir doğal sayının yanına reel sayılar kümesinde bulunan rastgele bir irrasyonel sayıyı yazıyoruz.

liste şuna benzer.

---

0 -> 0.1212341234343...
1 -> 0.2321232324544...
2 -> 2.2121281902812...
.
.
.
---

böylelikle her bir doğal sayı reel sayılar kümesindeki bir irrasyonel sayı ile eşleşmiş oluyor.

bu noktada kendimize şu soruyu soruyoruz.

reel sayılar kümesinin içerisinde arasak demin yazdığımız listede herhangi bir doğal sayı ile eşleşmemiş irrasyonel bir sayı bulabilir miyiz?

matematikçi olduğumuz için de denyo gibi sayı arayıp durmak yerine bu sayıyı yaratmayı tercih ediyoruz.

sayımızın ismi mahmut sayısı olsun.

mahmut sayısının ilk hanesi 0 sayısını eşleştirdiğimiz irrasyonel sayının ilk hanesinden bir fazla, ikinci hanesi 1 sayısını eşleştirdiğimiz irrasyonel sayının ikinci hanesinden bir fazla, üçüncü hanesi 2 sayısını eşleştirdiğimiz irrasyonel sayıdan bir fazla olacak diye diye mahmut sayısının her bir hanesini yazıyoruz.

yazdığımız mahmut sayısı kesin olarak bu listedeki eşleşmiş olan her bir irrasyonel sayının en azından bir hanesinden farklı olduğu için, listenin neresinde ararsak arayalım mahmut irrasyonel sayısının eşleştiği bir doğal sayı bulamayız.

mahmut sayısı reel sayılar kümesinin bir elemanı olduğu için de reel sayılar kümesinin sayılamaz, yani eşleştirilemez sonsuzluğa sahip bir küme olduğu, dolayısıyla eşleştirilebilir kümelerden eleman sayısı bakımından büyük bir küme olması gerektiği sonucuna varırız.

böylelikle sonsuzluk dediğimiz kavram olduğunu sandığımızdan çok daha karmaşık bir hal alır.