Matematikçi Gauss Mezar Taşına Neden Bir Onyedigen Çizilmesini İstedi?

antik yunanlılar geometri ustalarıydı ve özellikle bir pergel ve cetvelle oluşturulan yapılara özel bir önem vermişlerdi. ancak o dönemde kullanılan her iki aletin üzerinde de herhangi bir işaret yoktu. yani cetvel bir uzunluğu ölçmeye değil yalnızca düz bir çizgi çizmeye yarıyordu. benzer biçimde bir pergelle de yapabilen tek şey, merkezi verilen ve belli bir yarıçapa sahip çember çizmekti.

o dönemin matematikçilerinin amacı elbette matematiği zorlaştırmak değildi. aslında bir geleneği devam ettirmeye çalışıyorlardı. çünkü pergel ve cetvelle şekiller oluşturma oyunu, şimdiye kadar yazılmış en önemli ders kitaplarından biri olan öklid'in elemanlar kitabında yer alıyordu.

mö 300 civarında kaleme alınan öklid'in elemanları şimdiye kadar yayınlanmış en etkili matematiksel incelemedir. metinler büyük ölçüde geometriye odaklanır. ancak sanıldığının aksine bu kitap salt bir geometri kitabı değildir. aslında bu 13 ciltlik eser, yunanlılar tarafından bilindiği şekliyle tüm matematik dünyasını kapsamaktadır. kitabın en önemli özelliği kaynakları ele almasında ve düzenlemesinde yatmaktadır.]

öklid, geometrik nesnelerin varlığını yalnızca iddia etmek yerine,bunları açıkça en basit bileşenlerden, yani çizgiler ve dairelerden inşa etmek istemişti.

pergel ve cetvelle herhangi bir üçgeni oluşturmak kolaydır. sonucunda yapmanız gereken tek şey bir sayfanın üzerine üç tane rastgele nokta koymak ve daha sonra bu noktaları çizgiler ile birleştirmek olacaktır ancak mükemmel simetrik şekiller çizmek isterseniz durum değişir. düzgün çokgenler, tüm kenarlarının eşit uzunlukta ve tüm açılarının eşit ölçüde olması açısından en fazla simetriye sahip şekillerdir.

öklid, eşkenar üçgenler, kareler ve düzenli beşgenlerin nasıl çizileceğini kitabında göstermişti. daha sonrasında da bu temel yapılardan birkaç genelleme çıkarmıştı.

detaylarını açıklamasa da düzgün bir çokgenin kenar sayısını iki katına çıkartmanız durumunda, ortaya çıkan şeklin yeni bir düzgün çokgen olduğunu da yazmıştı. bu, üç, dört ve beş kenarlı düzgün çokgenlerin altı, sekiz ve 10 kenarlı düzenli çokgenlere ve ayrıca 12, 16 ve 20 kenarlı çokgenlere dönüştürülebileceği anlamına geliyordu.

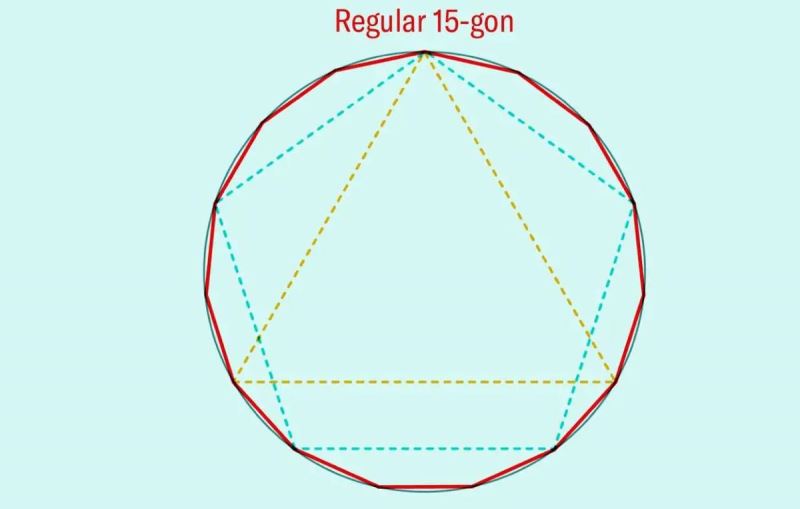
öklid üç ve beş kenarlı düzenli çokgenler ile 15 kenarlı bir çokgenin nasıl üretileceğini de göstermiştir. ancak ilerleme burada durmuştu. öklid, prensipte düzenli 3.072-geni inşa etmenin mümkün olduğunu söylüyordu ama düzenli bir 7-genin veya 11-genin nasıl inşa edileceği hakkında hiçbir fikri yoktu.

bu durumda

“hangi düzgün çokgen cetvel ve pergel ile çizilebilir?”

sorusu, iki bin yıl boyunca cevapsız kalacaktı. aslında uzun süre cevapsız kalması da matematik dünyası için bir şanstı. çünkü bu sayede carl friedrich gauss ile tanışacaktı.

30 mart 1795 sabahı, henüz 18 yaşında olan gauss, yataktan düzgün bir onyedigeninin nasıl çizileceğini bularak kalkmıştı. o kadar heyecanlanmıştı ki bu bulgusunu hemen günlüğüne yazdı. kendisi bu buluşuyla profesyonel matematikçi olmaya da karar vermişti. üstelik bu sonuca hiç düzgün onyedigen çizmeden ulaşmıştı.

bu büyük başarısının ardından gauss düzgün onyedigen çizme yöntemini bir kurama dönüştürdü. tahmin edileceği üzere ortaya koyduğu kuramı, bir kaç paragraf ile bir yazıda anlatmak olası değildir. eğer iş zaten bu kadar kolay olsaydı, bu soru 2000 yıl boyunca çözümsüz kalmazdı.

antik yunan'lıların geometrik şekilleri çizmek için kullandıkları ilkel araçlar, modern cebirin doğal işlemleriyle yani toplama, çıkarma, çarpma, bölme ve karekök alma ile mükemmel bir şekilde uyuşmaktadır. bunun nedeni, doğrular ve daireler için denklemlerin yalnızca bu beş işlemi kullanmasıdır.

ancak işler bazı düzgün çokgenlerin çiziminde karışacaktır. örneğin düzgün yedigen ve onbirgen çiziminde sorun çıkacaktır. bunun nedeni pi ya da 2'nin küp kökü gibi bazı sayıların toplama, çıkarma, çarpma, bölme veya karekök işlemleriyle ifade edilememesidir.

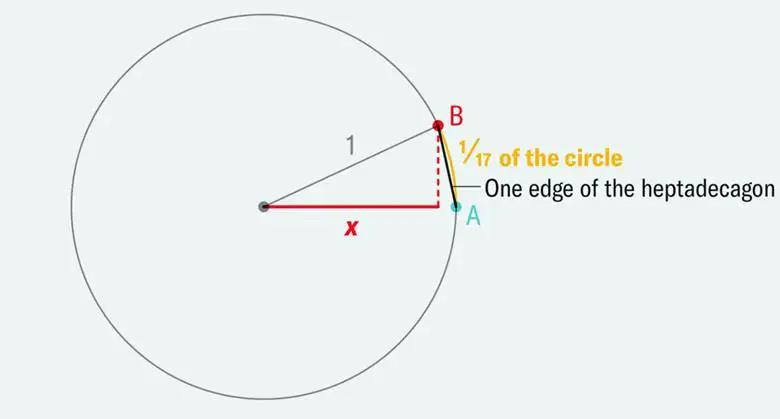
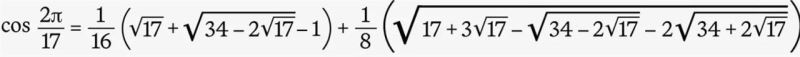
ifade oldukça karışık gibi gözükse de bu ifade sadece tamsayılara ve toplama, çıkarma, çarpma, bölme, karekök alma gibi temel işlemlere bağlıdır. bu nedenle de cos (2? /17) çizilebilir. bu da bize düzgün bir onyedigenin sadece cetvel ve pergel yardımı ile çizilebileceğini gösterir.

sonuç olarak gauss binlerce yıllık problemi çözmekten büyük gurur duymuştu. iddiaya göre bir arkadaşına mezar taşında düzenli bir onyedigen olmasını istediğini söylemişti.

ne yazık ki onun bu isteği gerçekleşmedi. ancak gauss'un doğum yeri olan almanya'nın brunswick kentindeki bir anıtın arkasında 17 köşeli bir yıldız yer almaktadır.

kaynaklar: scientificamerican.com, youtu.be