İnsanı Matematiğin Doğası Üzerine Düşünmeye Zorlayan Banach Tarski Teoremi
matematik ilminin en şaşırtıcı teoremlerinden biridir banach tarski teoremi.
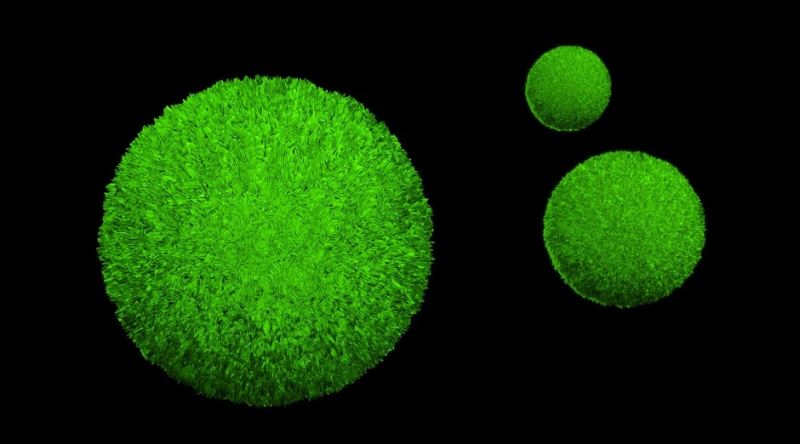
bildiğimiz üç boyutlu uzayda, farklı çaplarda ve içi dolu a ve b küreleri verilmiş olsun. banach-tarski teoremi der ki; a küresini sonlu sayıda parçaya bölüp, parçaları (hiç esnetip büzüştürmeden) değişik şekilde tekrar bir araya getirerek b küresini oluşturabiliriz.
yani bezelye büyüklüğünde bir küreyi sonlu sayıda parçaya bölüp, parçaları tekrar birleştirerek güneş büyüklüğünde bir küre yaratmak mümkündür! (bu meşhur bir örnektir, bu yüzden banach-tarski teoremi'ne bazen bezelye-güneş teoremi de denir.) tabii fiziksel olarak böyle bir olay mümkün değildir, bahsedilen parçalar "hacimsiz" parçalardır çünkü. sıfır hacimli değil; hacimsiz, yani hacmi tanımlanamayan parçalar...
öyle şaşırtıcı bir teoremdir ki bazen paradoks da denir buna. ama aslında paradoks falan değildir, doğruluğu bal gibi kanıtlanmış bir önermedir. kanıtın geçerliliği, seçme aksiyomunun doğruluğuna dayanır. sırf bu teorem yüzünden seçme aksiyomunu reddeden matematikçiler vardır. ama çoğunluk yine de seçme aksiyomunu (ve dolayısıyla banach-tarski teoremini) doğru kabul eder.
insanı gerçekliğin ve matematiğin doğası üzerine düşünmeye zorlayan bir teoremdir, oha dedirtir.