Fransız Bir Matematikçinin 1883'te İcat Ettiği Problem: Hanoi Kuleleri
Nedir bu problem?
hanoi kuleleri, fransız matematikçi edouard lucas tarafından 1883 yılında icat edilmiş bir problem.
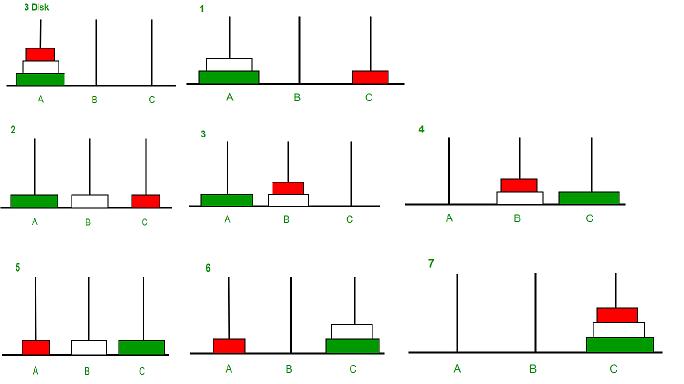
bir çubuğa geçirilmiş 8 adet diskin diğer bir kuleye geçirilmesi esasına dayanır bu problem. söz konusu 8 disk, büyükten küçüğe doğru üst üste birinci kuleye dizilmişlerdir. boş olan iki kule kullanılarak (yani toplamda 3 kulemiz var) en sağdaki boş kuleye bütün diskleri sıralı olarak transfer etmemiz istenir. aynı anda sadece bir diski bir kuleden diğerine geçirebiliriz ve bu disk en üstte duran disk olmalıdır. transfer edilen disk, başka bir diskin üzerine konulabilir, ancak altta kalan diskin her zaman üstteki disklerden büyük olması zorunludur.
Nasıl çözülür?
diyelim ki n tane diskin hepsini bir başka çubuğa dizmek için gerekli hamle sayısını veren fonksiyon h(n) olsun. büyük diskin üzerine küçük disk gelemeyeceği için öncelikle büyük diskin üzerindeki tüm diskleri başka bir çubuğa taşımalı, en büyük diski yalnız bırakmalı ve bir de boş çubuk bırakmalıyız ki bir sonraki hamlede en büyük diski taşıyalım. fakat bu aslında, bu oyunu n-1 tane diskle (baştan sona) oynamakla tam olarak aynı şeydir. elbette ki n-1 tane diski taşımak için gerekli hamle sayısı h(n-1) olacaktır.
şimdi en büyük diskimizi boş çubuğa taşıyalım. bir hamle daha yaptık. şimdi üst üste duran n-1 diski büyük diskin üzerine taşımalıyız. fakat bu da tam olarak bu oyunu (baştan sona) n-1 disk ile oynamakla aynı şeydir. yani tekrar h(n-1) hamle yaptık. o halde h(n) = h(n-1) + 1 + h(n-1) = 2 h(n-1) +1 eşitliğini elde ederiz. ama benzer şekilde h(n-1)=2 h(n-2)+1 olmaz mı?
h(n) = 2 h(n-1)+1
= 2(2 h(n-2)+1)+1 = 4 h(n-2)+2+1
= 4(2 h(n-3)+1)+2+1 = 8 h(n-3)+4+2+1
.
.
.
böyle böyle h(n-(n-1))=h(1)'e kadar gider bu iş.
=2^{n-1}h(1)+2^{n-2}+2^{n-3}+...+4+2+1
h(1)=1 olduğu gayet açık ve sarih. e, o halde
h(n) = 2^{n-1}+2^{n-2}+2^{n-3}+...+4+2+1=(2^n)-1 eşitliğini bulur ve muradımıza ereriz. sonda üstsel bir fonksiyon bulunduğu için yazılım ve donanımı kıyaslamada güzel bir örnektir.
1969'dan Beri Çözülemeyen Sağlam Bir Problem: Newcomb Paradoksu
