Bir Yolu Asla Katedemeyeceğinizi Söyleyen Enteresan Bir İkilem: Aşil Paradoksu
ilk çağ felsefecilerinden elea okulunun en önemli ikinci filozofu (birinci filozof (bkz: parmendies)) zenon'un öne sürdüğü bir paradokstur.
zenon'a göre haraket imkansızdır, bunu da belirli bir zaman içinde hiçbir mesafenin aşılamayacağını düşüncesi üzerine söyler, bir paradoks yaratır:
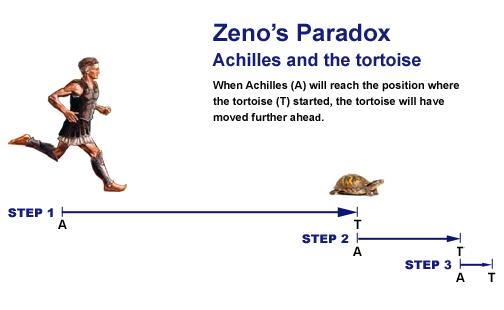
iddia
aşil kaplumbağaya her yaklaştığında kaplumbağa da bir mesafe alacağı için başka bir noktaya ulaşacaktır, böylece bir doğrunun sonsuz sayıdaki noktadan oluştuğu varsayımına göre asla geçemez, geçebilmesi için sonsuz bir mesafeyi sonlu bir zaman zarfında alması gerekir.
çözümü
öncelikle basit bir matematikle bu sorun çözülebilir, aşil'in hızı 10 m/s kaplumbağanın hızı ise 1 m/s olsun ve 100m avans ile önde başlamış olsun. katedilen süreyi de t olarak belirtelim
10*(t) = 1*(t) + 100 hesaplamasına göre 11.11 sn sonra aşil kaplumbağayı yakalayacaktır. başlıktaki sonsuz ıraksama yönetimiyle de çözülebilir.
peki zenon bu çözümü bilmiyor muydu, en nihayetinde pratikte aşil'in kaplumbağayı yakalayacağını biliyordu ona göre gözlem-pratik ile matematiksel felsefenin bakış açısının başka başka şeyler olduğu yönündedir.
çıkarttığımız sonuçlara göre değerlendirmeleri yapalım
zenon matematiksel-felsefe açısından kesinlikle haklıdır ama örneği yanlıştır bugün biliyoruz ki uzay zaman içinde matematik ve fizik kullanarak her şeyi hesaplayabiliyoruz. einstenin görelilik kanuna göre tüm hızlar, bir referans çerçevesine göre ölçülür. (bkz: referans çerçevesi)
ama örneğin programlama yaparken kullanılan recursive fonskiyonlarda zenon'un paradoksu çalışır, sonsuz döngüye girer.
buradan da anlaşılacağı gibi zenon'un asla yakalayamaz ifadesindeki asla kelimesi yanlıştır, ortama göre değişebilir.
Satın Alması İmkansız Olan ve İçinde Bir Cin Bulunan Bir Şişeyi Konu Alan Paradoks
