Alemin En Delikanlı İki Dağılımından Biri: Poisson Dağılımı

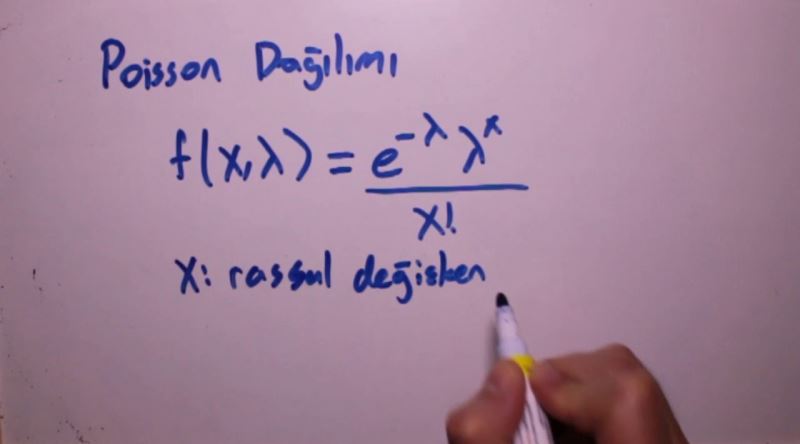
poisson dağılımı, alemin en delikanlı iki dağılımından biridir, en az kendisi kadar karizmatik olan kardeşi de geometrik dağılımdır. peki neden herkesin bildiği, sevdiği, saydığı güzelim gaussian varken bu iki dağılıma delikanlı dedik? çünkü memoryless özellikleriyle, karışık matematikten bunalan mühendislerin imdadına koşarlar, exponentialların 21. yy'daki önemlerini bize kanıtlarlar.

şimdi bütün bunlar ne demek oluyor, memoryless nedir, yenir mi, üniter yapıyı bozar mı? efendim diyelim otobüs bekliyorsunuz, 10 dakika içinde geleceğinden eminsiniz, lakin tam olarak ne zaman geleceğini bilmiyorsunuz. iyice hayattan bezmiş uyuşuk biri olduğunuz için de ancak dakikada bir defa kafanızı kaldırıp otobüsün gelip gelmediğine bakıyorsunuz. şimdi otobüsün gelişi eğer uniform dağılıma sahipse, her on gözlemizde otobüsün gelmiş (ve belki de çoktan gitmiş) olması eşit ihtimallere sahiptir, yüzde 10dur. şimdi ben havuz sorularından sıkılan sizleri eğlendirmek için durağa yanaşıyorum ve görüyorum ki 6. dakikada halen otobüsün gelmemiş olduğunu farkediyorum. o zaman otobüsün 7, 8, 9 ve 10. dakikada gelme olasılıklarının dağılımı değişir mi? değişir tabii, bal gibi değişir.

oysa orijinal dağılımımız poisson olsaydı değişmezdi. nedeeen, çünkü poisson dediğin lambda*exp(-lambda*t) dir, eğer t zamansa. lambda dediğin bu olayın rate'i. exponentialdaki eksiye dikkat edersek, lambdamız ne kadar büyükse, olayımızın gerçekleşme ihtimali de başlarda (t küçükken) o kadar büyük, t ilerledikçe de o kadar hızla düşer. yani kalantör bir lambdamız varsa, otobüsün ilk 2 dakikada gelme ihtimali yüzde 95 iken, ikinci ila dördüncü dakika arasında gelmesi yüzde 3, dört ile altı arası binde 5, vs diye exponential olarak azalabilir. işte bu exponential eğrinin biçimi, siz otobüsün ilk altı dakikada gelmemiş olduğunu keşfetseniz bile sonraki zamanlar için değişmez, sadece 7 8 9 ve 10. dakikalarda gelme ihtimallerinin toplamı 1 (yahut yüzde yüz) olacak şekilde scale edilir. memoryless'lik budur ve en asıl duygunun özelliğidir.

continuous timeda memoryless olan tek dağılım poissondir (discrete alemlerde ise geometrik. aslında önceki örnekte otobüsün gelişini ancak dakikada bir gözlemlediğimiz için bu discreete bir örnektir ama çaktırmayın)

şimdi bu lambda parametresi önemli, çünkü her durumda sabit kalmıyor. yani diyelim lambda dediğimiz şey, zamana bağlı bir fonksiyon olsun, örneğin 4x-x^2+17 olsun da bir halta benzemesin. e ne oldu şimdi, zaman ilerledikçe, exponentialın düşüş hızı da değişecek, kah neşeli kah hüzünlü davranacak. işte buna da non-homogeneousluk denir.

iki poisson biraraya gelirse samanlık seyran olur atasözünü hatırlamamızda fayda var. bundan kastımızı naçizane örneğimize devam ederek anlatalım. durakta otobüs bekliyorsunuz hala ama otobüs dediğin tek tip değil. bildiğimiz biletli iett otobüslerinin yanında, melih gökçek'in yeşile boyamak suretiyle vatandaşa doğal gazlı diye yutturduğu rivayet edilen ve paralı olan otobüsler de mevcut. bu iki tip otobüs ayrı çizelgelere sahip ve biri ortalama olarak saatte iki defa gelirken, ötekisi üç defa geliyor. şimdi yavaş yavaş yanan ampulunuzun de işaret ettiği üzere, ortalama olarak bu durağa saatte beş otobüs geliyor. ama ortalamayı bilmekle tüm dağılımı bilmek farklı şeyler. sonuçta saatte birden ona kadar ki tüm otobüs sayısının uniform olması durumunda (yani her birinin yüzde on ihtimali olması durumunda) da ortalama 5tir, poissonda da olabilir, uygun bir rayleighde de. dolayısıyla kırmızı otobüslerimize bakarsak, saatte ortalama üç otobüs bilgisiyle bu dağılımı poisson olarak modellediğimiz takdirde, herhangi bir t zamanda otobüs gelme ihtimali 3*exp(-3*t)dir. diğer otobüsün ki ise 2*exp(-2*t)dir. şimdi poisson'ın güzelliği, bu iki ayrı süreci birleştirdiğimizde, yani hangi otobüs olduğu farketmez biletim de var param da bu alemin kralıyım dediğimizde, sadece saatte gelen ortalama otobüs sayımız 3+2=5 olmakla kalmıyor, bir de dağılımımız 5*exp(-5*t) formülünün belirttiği eğriye denk geliyor. t yerine 3.1416inci saniyeyi koyarsanız, bu vakitte herhangi bir otobüsün gelmiş olma ihtimalini bulursunuz.

işte böyle güzeldir poisson, ekle çıkar çarp bol hiçbir şey demez, hafızasını yitirmiştir zaten, umrunda değildir. poisson'a gereken saygıyı gösterelim, gaussian gibi kabadayılar karşısında ezilmesine müşahade etmeyelim.

Başka bir anlatımla

poisson (puason diye okunur) dağılımı neleri varsayar?

1-) herhangi bir zaman noktasını seçersek, bu noktadan sonraki gelecek bu noktadan önceki geçmişten bağımsızdır. deneyin görün nasıl da sadeleşiyor o güzel exponentialcikler...

2-) poisson vukuat sayısının 54 kere olmasının olasılığını verir. ya da 34 kere olmasının. kısaca x kere olmasının. bu x kere olmasının olasılığını adam gibi (unbiased)^* hesaplayabilmek için bi de demeliyiz ki:
herhangi bir anda^* sadece bir tane olay olabilir ya da olmaz. (yani aynı anda mükerrer olmaz)

3-) olaylar birbirinden bağımsız gelişir.

şimdi toparlayalım bakalım: neymiiiş, zaman noktası değiiil zaman dilimi önemliymiş. yani belli bir zaman intervali içerisinde hesaplıyacağız bu olasılıkları (x kere vukuat olmasının olasılığı).

hemen bir örnekle karışmış beyinleri ütüleyelim, düzlüğe kavuşturalım:

ahmet abi mahallemizin güzel abilerindendir. velinimet ise mahallenin zillisidir. velinimete ortalama günde 40 herif girmektedir. velinimetin 24 saat çalıştığı ve velinimete girişlerin poisson olduğu düşünülürse, 1 saatte karıya 4herif girmesi olasılığı nedir?

hemen formüle (bkz: #1924214) bir bok atalım ve düzeltilmişini sunalım sonra da oturtalım ve görelim.

f(x) = exp(-1*lambda*t) * (lambda*t) ^x / x!

siz şimdi sibopluk yapıp anlamazsınız da bu formülü sizi gidi ampirikukular sizi.

lambda: zaman birimi başına ortalama giriş (burada 40 herifin 24 saatte girdiği düşünülürse hemen bölünür (zaman noktasından bağımsızlık özelliği) ve saatte 40/24 herifin girdiği anlaşılır)

t: zaman intervali (burada bir saatte 4 kişi girmesi ihtimali soruldu o yüzden t=1)

x: vukuat sayısı (istiklal marşı okunması adedi)

f(4) = exp(-1*40/24*1) * (40/24*1) ^4 / 4! = 0.0607

bu cevabı bulanlar bokunda boncuk bulmuş gibi sevinebilirler. bunla yetinmeyenlere ise bir tane daha finansal soru:

ahmet abi kapının önünde kankası hikmet'le durmaktadır. ahmet abinin ziki dikilmeye başladığından beri 1 saattir ne gelen vardır ne giden. ahmet abi hikmet'e "ulan yarım saatte kadar bi herif gelmezse velinimete ben girecem".
ahmet abinin mala vurma olasılığı nedir?

şimdi önemli varsayımları kullanalım. ahmet abinin mala vurması için önümüzdeki yarım saat kimsenin gelmemesi lazımdır. ama bi saattir zaten kimse gelmemiştir. o zaman belirtilen zaman intervali için 0 adam gelmesi olasılığını hesaplayalım ve direk ahmet abiyi gönderelim.
bu zaman intervali ne kadar peki? sizi kefaller. nah bir buçuk saat! ne demiştik? belli bir zaman noktası belirtildikten sonraki vukuatler öncekilerden tamamen bağımsızdır. yani biz önümüzdeki yarım saat 0 adam gelmesi ihtimalini hesaplayacağız. inanmayan conditional probability hadiseleriyle bunu görebilir.
t=1/2
f(0) = exp(-1*40/24*1/2) * (40/24*1/2) ^0 / 0! = 0.4346

böyle 0 tane olay olması veya 1 tane olay olması gibi sorularda dikkati çeken bir nokta ise f(1) = exp(-1*lambda*t) * (lambda*t) şeklinde formülümüzün sadeleşmesidir. biz buna exponential distribution diyoruz. poisson'daki vukuatlerin arasındaki zaman aralıkları exponentially distributed olmak gibi bir özelliğe sahiptirler.

işte böyle bu poisson.

bir çok dağımın buna yakınsadığı rivayet edilir. mesela binomial dağılımda n ve p kullanılarak poisson approximation yaratılabilir. ama poisson'un felsefesi farklıdır. öyle yakınsamalar bozar onu.