0 Faktöriyel Neden 1'e Eşittir?
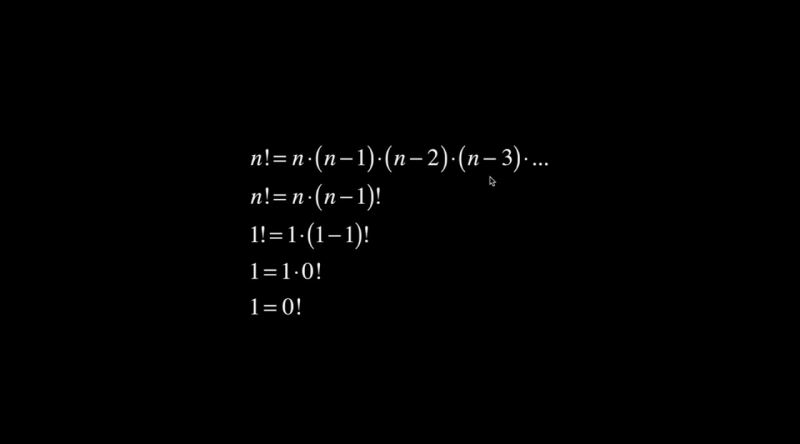
açılın ben doktorum, şey öhöm matematik öğretmeniyim
artık yeni ortaokul matematik programında faktöriyel, permütasyon ve kombinasyona yer verilmiyor. eski programla ders işlenirken sıfır faktöriyelin neden bir olduğunu soran öğrencilerime durumu şöyle izah etmeye çalışıyordum:
a, b ve c isimli 3 kişi (hep birlikte) panonun önünde yan yana fotoğraf çektirmek istiyoruz. kaç farklı sıralamayla fotoğraf çekinebiliriz? abc, acb, bac, bca, cab, cba şeklinde 6 tane (yani 3!=6) fotoğraf çekimi yapılabilir.
a ve b isimli 2 kişi (hep birlikte) yan yana fotoğraf çektirmek istiyoruz. kaç farklı sıralamayla fotoğraf çekinebiliriz? ab ve ba olmak üzere 2 tane (yani 2!=2) fotoğraf çekimi yapılabilir.
a kişisi tek başına fotoğraf çekinmek isterse tek bir sıralamayla (1!=1) fotoğraf çekilebiliyor.
peki elimizde hiçkimse olmadığında kaç fotoğraf çekilebilir? fotoğraf çektiğimiz panonun boş bir fotoğrafını çekebiliriz. daha öncekilerde kümenin tüm elemanlarını kullanarak yapılacak sıralama sayısının faktöriyele eşit olduğunu göstermiştik. küme boş olduğunda da boş haldeki pano önünde bir fotoğraf çekebiliyoruz. o halde 0! = 1'dir diyordum.
bunun matematiksel olarak bir ispat olmadığını biliyorum tabii ki ancak ortaokul düzeyinde öğrencilere bu şekilde verdiğimde faydalı olduğunu düşünüyordum. dediğim gibi, artık programdan kaldırıldığı için lise öğretmenlerine atıyoruz topu.
küçük bir örnekle neden kendisini 1 kabul etmek matematikçilerin işine geliyor anlatmaya çalışayım
elimizde basit bir s kümesi olsun s={kedi, köpek}
bu kümenin alt kümeleri nelerdir desek :
- boş küme
- {kedi}
- {köpek}
- {kedi,köpek}
şeklinde listeleyebiliriz.
listenin son elemanı, yani kümenin kendisi de bir alt küme malumunuz.
bir s kümesi içinden r elemanlı kaç alt küme çıkar şöyle buluyoruz.
* n=ana kümenin eleman sayısı,
* r=kaç elemanlı alt küme isityoruz
olmak üzere
combination(n,r)
şimdi 2 elemanlı bu kümeden 2 elemanlı alt kümeyi, yani kendisini çekelim.
combination(n,r) = n! / (n-r)! * r! olmak üzere
combination (2,2) = 2! / (2-2)! * 2! = 1!/0!
tam bu noktada 0!'ü 1 kabul ettiğimiz zaman 1/1 = 1 sonucuna erişmiş oluyoruz.
nitekim de zaten n elemanlı her s kümesinin bir tane n elemanlı alt kümesi olabilir o da kendisi.
not: neden permutasyon değil de kombinasyon? çünkü özel bir durum belirtilmedi ise s={kedi ,köpek} = {köpek, kedi}
sıralamayı değiştirmek kümeyi değiştirmiyor.
bunun için kombinasyon alıyoruz.
mesele kabaca bundan ibaret. ali hoca bu konuyu 2 videoluk bir seride, uzun uzun, ve elbette ki benden kat kat derin şekilde anlatıyor. özellikle ispatlar neden yanlıştır onu gösteriyor. izlemenizi öneririm.


